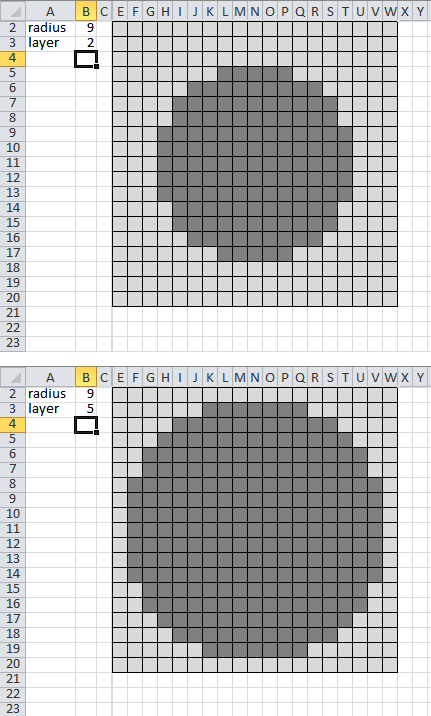
Before I get out the glue, how would I go about creating a spreadsheet that would show me the quantity and placement of cubes in each cross-sectional layer? (think of an MRI scan cross-section)
For input, the spreadsheet should ask for the radius of the sphere to be built, as well as which layer of that sphere should be displayed.
There may be more than one way to accomplish this. Any spreadsheet that will allow me to build a sphere by displaying each layer of a sphere for a given radius is considered valid.
Here is an example of output:
Hint: The formula for distance in 3 dimensions is:
d=√[(x2-x1)2+(y2-y1)2+(z2-z1)2]
Bonus question! Adjust your algorithm to display a hollow sphere (think of a ping pong ball, or a beach ball). Note: All cubes must be connected into one contiguous piece.



