I would like to construct a sphere by gluing unit cubes together. I'm only attempting to approximate the shape of a sphere as closely as is possible with unit cubes.
Before I get out the glue, how would I go about creating a spreadsheet that would show me the quantity and placement of cubes in each cross-sectional layer? (think of an MRI scan cross-section)
For input, the spreadsheet should ask for the radius of the sphere to be built, as well as which layer of that sphere should be displayed.
There may be more than one way to accomplish this. Any spreadsheet that will allow me to build a sphere by displaying each layer of a sphere for a given radius is considered valid.
Here is an example of output:
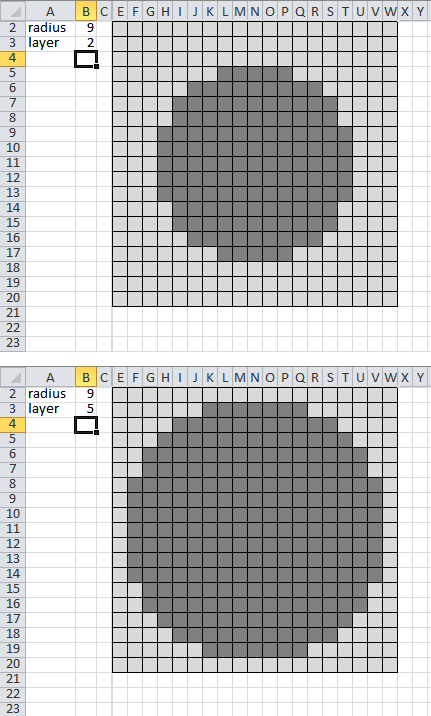
Hint: The formula for distance in 3 dimensions is:
d=√[(x2-x1)2+(y2-y1)2+(z2-z1)2]
Bonus question! Adjust your algorithm to display a hollow sphere (think of a ping pong ball, or a beach ball). Note: All cubes must be connected into one contiguous piece.
(In reply to
Bonus thoughts by Steve Herman)
Steve,
I tried the formula that you gave for a), works nicely!
I did notice that you made mention of using even numbers of layers when making an earlier comment. You will notice that Dustin's images and my javascript emulations use odd. The nett result is that you have valid solutions for even layering as opposed to us working with odd.
After revisiting your "hollow" sheet I edited the latter part of your formula:
<=POWER($B$2-1.5,2),"","X"),"")
<=POWER($B$2-1,2),"","X"),"")
You had 1.5, I made it 1. It would use less cubes, I tested it with the radius = 3 in both cases. Are there any radii where my edit would create issues?
Edited on February 26, 2012, 9:00 pm
|
|
Posted by brianjn
on 2012-02-26 19:58:05 |




