If you drew a dot on the edge of a wheel and traced the path of the dot as the wheel rolled one complete revolution along a line, then the path formed would be called a cycloid (shown below), combining both forward and circular motion.

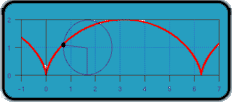
If a wheel of radius 1 traces out such a path, what is the length of the path formed by one complete revolution?

Taking an approach similar to friedlinguini, I considered the motion to be a combination of movement around a circle clockwise starting from the bottom and translation in the x direction. So in the y direction there is no contribution from the horizontal translation.
call the angle t (as in theta)
dy= sin(t) dt
dx= (1-cos(t)) dt
the arc length S is found by integrating ds
ds^2=(dx^2+dy^2)=sin^2 + 1 + cos^2 -2cos=2(1-cos(t))
so S=the integral from 0 to 2π of √[2(1-cos(t))] dt

which is where I got stuck
but friedlinguini is correct
the arclength is 8
the horizontal distance travelled is 2π

Posted by Larry on 2004-02-21 14:26:04