Begin with an arbitrary, convex quadrilateral. Next, draw squares outwardly on the sides of the quadrilateral, and join the centers of opposite squares.

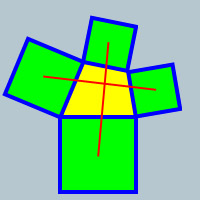
You might find the the two resulting lines are equal in length and intersect at precisely 90 degrees.

Prove (or disprove) the notion, that this is always true.

(In reply to Small problem by Sam)

>>I wonder if someone can provide us with a more intuitive proof then the one Federico linked?

My approach was going to use analytical algebra (Cartesian geometry), and thus would have been similar to the proof Federico linked to.

It can also be done with Euclidean geometry as well, by constucting intermediate congruent triangles

Posted by TomM on 2004-01-10 13:27:36