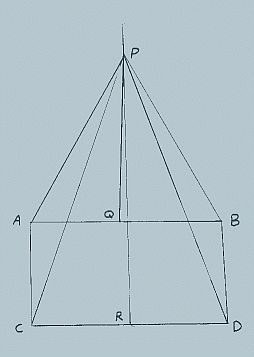
- In the figure, above AC=BD.
- ‹ACD is a right angle.
- ‹BDC is less than 90º.
- QP and RP are perpendicular bisectors of AB and CD respectively, intersecting at P.
- AP=BP and CP=DP because all points on the perpendicular bisector of a line are equidistant from the extremities of the line.
- Triangle APC is therefore congruent to triangle BPD because of the well known "side-side-side" theorem.
Now, ‹PCD=‹PDC because the base angles of an isosceles triangle are equal.
- ‹ACP=‹BDP because they are corresponding parts of congruent triangles.
- Of course, ‹ACP + ‹PCD = ‹BDP + ‹PDC because when equals are added to equals the results are equal.
But, wait, we know that this isn't true!
A mathematician had a rickety table (with top AB sitting on the floor CD with legs AC and BD) and had constructed the drawing above in an ineffectual effort to straighten the table. Can you figure out what is wrong?



