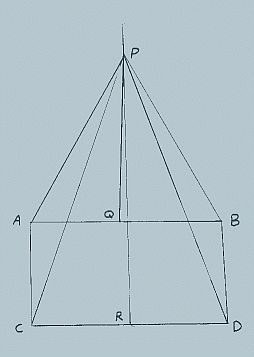
- In the figure, above AC=BD.
- ‹ACD is a right angle.
- ‹BDC is less than 90º.
- QP and RP are perpendicular bisectors of AB and CD respectively, intersecting at P.
- AP=BP and CP=DP because all points on the perpendicular bisector of a line are equidistant from the extremities of the line.
- Triangle APC is therefore congruent to triangle BPD because of the well known "side-side-side" theorem.
Now, ‹PCD=‹PDC because the base angles of an isosceles triangle are equal.
- ‹ACP=‹BDP because they are corresponding parts of congruent triangles.
- Of course, ‹ACP + ‹PCD = ‹BDP + ‹PDC because when equals are added to equals the results are equal.
Therefore, ‹ACD = ‹BDC.
But, wait, we know that this isn't true!
A mathematician had a rickety table (with top AB sitting on the floor CD with legs AC and BD) and had constructed the drawing above in an ineffectual effort to straighten the table. Can you figure out what is wrong?
Think of a top down view. Point A is directly above point C so they appear to be one point. Also, line CP is is diectly above AP. So far in this veiw you have one straight line. Now draw a second line of equal length to show angle APB. Draw a third line of equal lenght just a few degrees off of PB to show angle CPD. Now complete both isosceles triangles by drawing AB and CD. The solution is as I stated before. ABDC is not a quadralateral rather AD is the line of intersection between plane ACD and ABD. Vertex D has 4 serfaces and point P is shared by the triangles. Think of it this way. You can make AP any length as long as BP is the same. Also, you can make AB any length without regard to CD. By changing AP and AB you can always place point A diectly above point C and still have 2 isosceles triagles sharing point P no mater where in space P may lay. Do you self a favor, draw segment AD!
By the way. If I wanted to find the angle to straighten the table leg show as BD I wouldn't even focus on vertex D but vertex B so when I got an angle to correct by it would be based on the table top and not the angle of another lag to the floor. Angles to the floor change as you straighten legs! This means you need to fold the quad on the BC line of intersecting planes. But this is another problem.




