You may find this problem similar.

In a cube of side 4, I pack eight spheres of unit radius.

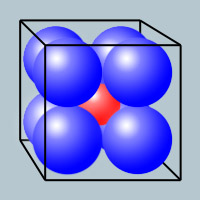
What is the largest sphere I can place in the center (such that it doesn't overlap any of the other spheres)?

the cube is 4x4x4. the farthest corners are then √(4²+4²+4²) or √48.

the spheres are 2 units in diameter each. they take up a total of 4 units of the √48 distance. which leaves (√48 - 4) of gap. half of this space is between them and half is at the corner.

my solution is (√48-4)/2 for a diameter or (√48-4)/4 for a radius.

r=0.73205...

Posted by superfuous_nut on 2004-02-10 18:54:03