You may find
this problem similar.
In a cube of side 4, I pack eight spheres of unit radius.
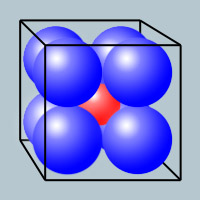
What is the largest sphere I can place in the center (such that it doesn't overlap any of the other spheres)?
if we take the shape in 2d(a XY plane in the middle of the cube,where is the max circle of the spheres) and draw a square with it's vertices on the center of the circles,it's side will have a length of 2 * radius = 2 so it's
diagonial will have length 2 * √2 .If after we draw a circle in the center of the empty space formed by the circles is diameter will be
square's diagonial - 2 * radius of the circle = 2 * √2 - 2 . so i believe that the same holds and for the cube in 3d
and that makes the radius of the central sphere equal to (2 * √2 - 2) / 2 = √2 - 1
sorry for my terrible english :)
|
|
Posted by John
on 2004-02-13 12:24:38 |



