You may find
this problem similar.
In a cube of side 4, I pack eight spheres of unit radius.
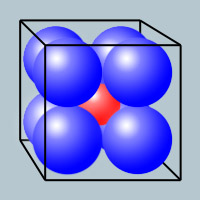
What is the largest sphere I can place in the center (such that it doesn't overlap any of the other spheres)?
As several people have posted, I agree that the answer is √3-1. Here's a more general problem: I have an n-dimensional 'n-cube' of side 4. I pack 2^n 'n-spheres' of radius 1 packed in it, similarly to the 3 dimensional problem. What's the largest 'n-sphere' I can place in the centre? What happens as n gets larger?
Surprisingly, the radius of the inner 'n-sphere' increases with n, and for enough dimensions it will stick out of the sides of the 'n-cube'! If I'm not mistaken, it goes to infinity with n, but I'll have to do the calculation.
another dimension
