You may find
this problem similar.
In a cube of side 4, I pack eight spheres of unit radius.
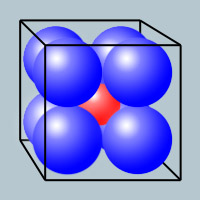
What is the largest sphere I can place in the center (such that it doesn't overlap any of the other spheres)?
(In reply to
re: another dimension by SilverKnight)
For an n-dimensional cube, side length 4, with 2^n hyperspheres inside it with radius 1, the radius of the hypersphere fitting inside is √n-1 (As SK said).
This is because the diagonal accross the cube is √(n4²). Subtracting the lengths from the corner to the point at which the hyperspheres touch the center hypersphere, I get √(n4²)-2*(1+√(n4²)/4). This simplifies to 4√(n)-2-2√(n)=2√n-2. The radius is then √n-1.
For the center sphere to reach the sides of the cube, I'd say it takes 9 dimensions. I'm having trouble imagining such a cube, but I think that these "sides" would have 8 dimensions themselves.
|
|
Posted by Tristan
on 2004-02-13 15:01:39 |
re(2): another dimension
