You may find
this problem similar.
In a cube of side 4, I pack eight spheres of unit radius.
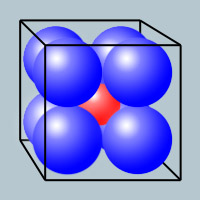
What is the largest sphere I can place in the center (such that it doesn't overlap any of the other spheres)?
Instead of adding dimensions to the hexahedron why not just use other regular polyhedrons? Try 4 spheres in a tetrahedron or 6 in an octahedron. You could keep the size at 4 or the radius at 1 but not both. Ether way it's a task before you ever get to the extra sphere in the center. Now that I think about it 6 spheres in an octahedron is very easy if the radius is 1. OK try a dodecahedron or an icosahedron. ;8^)
Edited on February 15, 2004, 12:28 am
Edited on February 15, 2004, 12:31 am
Less otherworldly
