Remember
"Four Bugs" or
"Three Bugs"?
In this problem, the six bugs start at the corners of a regular hexagon (with side length=10 inches).
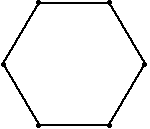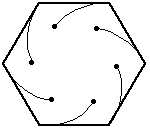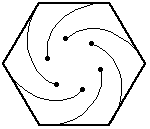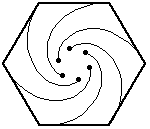
Again, the bugs travel directly towards their neighbor (counter-clockwise). And, again, each bug homes in on its target, regardless of its target's motion. So, their paths will be curves spiraling toward the center of the hexagon, where they will meet.
What distance will the bugs have covered by then, and how did you determine it?
Someone (Charlie I think?) went through this in one of
the previous problems.
The key is the instantaneous closing velocity between the
bugs. Consider the bug A at the bottom left. At the instant
they start, he heads to the right at a speed of 1 inch per second.
The bug B he is headed toward moves with a velocity of
(1/2, sqrt(3)/2). This means that A is approaching B at
a speed of 1/2 at that instant.
As the motion progresses, the relative positions change
but the angles never do. A will continue to approach B
at a rate of 1/2. This means they will meet in 20 seconds.
So each bug will have traveled 20 inches.
 Remember "Four Bugs" or "Three Bugs"?
Remember "Four Bugs" or "Three Bugs"?


