Remember
"Four Bugs" or
"Three Bugs"?
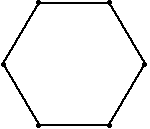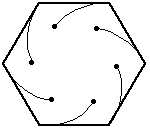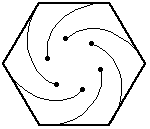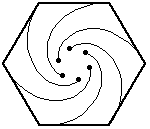
In this problem, the six bugs start at the corners of a regular hexagon (with side length=10 inches).
Again, the bugs travel directly towards their neighbor (counter-clockwise). And, again, each bug homes in on its target, regardless of its target's motion. So, their paths will be curves spiraling toward the center of the hexagon, where they will meet.
What distance will the bugs have covered by then, and how did you determine it?
(In reply to
Where's Penny by Richard)
Richard: "Penny must be on spring break or she probably would have already commented..."
It ain't Spring yet, dude. Besides, embarrassment over my many egregious blunders in that thread drove me to silence. I originally failed to distinguish between degrees and radians, resulting in an absurdly large result. Then Charlie had to tell me how to subtract negative numbers (it is very tricky...you have to add a positive number...), and even SilverKnight, who is usually my most ardent admirer, started to criticize me... :o)
But I did have the correct formula.
:-)
Edited on March 22, 2004, 1:19 am
|
|
Posted by Penny
on 2004-03-22 00:18:57 |
 Remember "Four Bugs" or "Three Bugs"?
Remember "Four Bugs" or "Three Bugs"?


