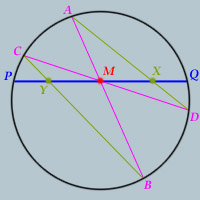
Given a circle and two points on that circle, P and Q, draw the chord PQ, and label its midpoint M.

Now draw two other chords of the circle AB and CD that both pass through M.

Further, draw chords AD and BC.

Label the intersection of AD and PQ, point X.
Label the intersection of BC and PQ, point Y.
_____________________________

Prove that M is the midpoint of line segment XY.

I'm stumped here.  Maybe if I start stabbing around...

Reflect MD over the diameter going through M.  Call this new segment MF.  Connect F to Y.  If our proof is true, then FY should be a reflection of XD.
....?

Can someone with more trigonometric experience tell me how angle CMP relates to the lengths CM and CD?

Call the center point O.  OM=OM, <OMY=<OMX... I just need to prove OY=OX...

Clearly, I'm desperate... Great puzzle!

Posted by Tristan on 2004-03-25 20:29:41