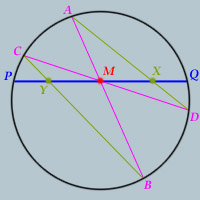
Given a circle and two points on that circle, P and Q, draw the chord PQ, and label its midpoint M.

Now draw two other chords of the circle AB and CD that both pass through M.

Further, draw chords AD and BC.

Label the intersection of AD and PQ, point X.
Label the intersection of BC and PQ, point Y.
_____________________________

Prove that M is the midpoint of line segment XY.

(In reply to re(2): stumper -- A Visual Guess by Thalamus)

I really did guess the word "butterfly" as a descriptive word that would possibly be used to describe this problem's configuration.  Googling chords midpoint alone does not zero in, but adding butterfly really does.  So my guess panned out.  If you have access to Coxeter & Greitzer, the proof they give is really nice, but is only one of at least a dozen quite different proofs that have been discovered over many years. I would say that proving this on ones own would distinguish one as a real geometer and not just some puzzle dilettante.

Posted by Richard on 2004-03-26 16:18:24