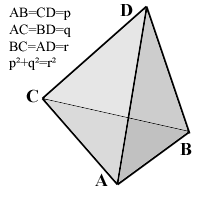
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with

AB=CD=p,
AC=BD=q,
AD=BC=r,
and p²+q²=r².

What's its volume, as a function of p, q and r?

There's the easy, insightful way, and the laborious spherical-trig way.  Of course I tried the latter first, but will present the former first:

ADB and ADC, being congruent right triangles with a shared hypotenuse actually can form a rectangle ACDB if laid out flat, with the hypotenuse, AD being a diagonal.  The other diagonal, CB, is of course equal to AD.  If the formed rectangle is then folded so as to form a dihedral angle at AD that is less than 180 degrees, C and B will come closer together than the distance from A to D.  But the puzzle requires that CB be as long as AD, so we can't unflatten the double triangle.  The other two triangles have to be flat on the other side, and the whole thing has collapsed into a flat tetrahedron of volume zero.

Now the way I first tried:

Erect a sphere about one vertex.  The face angles become sides and the edges become vertices, of a spherical triangle.  Label the triangle PQR with point P representing an edge of length p, etc.

Side PQ is length 90 degrees as it results from a 90-degree angle on the corresponding face. Its cosine is zero and its sine is 1, so the law of cosines reduces to

cos(QR) = sin(PR) cos P, where P is the dihedral angle at the edge with length p.

But cos(QR) = q/r and sin(PR) = q/r also, as defined by the plane faces, so cos P is 1 and so the dihedral angle at AB or CD is zero.  It's indeed a collapsed tetrahedron.

 

Edited on April 26, 2004, 9:53 am

Posted by Charlie on 2004-04-26 09:51:06