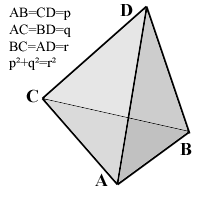
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with

AB=CD=p,
AC=BD=q,
AD=BC=r,
and p²+q²=r².

What's its volume, as a function of p, q and r?

Since A, B and C are on a same plane, put A at (0,0), B at (p,0) and C at (0,q). DC is perpendicular to AC, so D must be on a plane perpendicular to AC, which includes C. DB is perpendicular to AB, so D must also be on a plane perpendicular to AB, which includes B. The intersection of these two planes is a straight line, perpendicular to the ABC plane, which it intersects on (p,q). Finally, AD=r... but that's the distance from the origin to (p,q) so D lies on the same ABC plane, and the volume of this "tetrahedron" is zero.

Posted by Oskar on 2004-04-26 10:27:19