Below is an image of a square, 7 cm to a side, with four quarter-circles inscribed into it as showm.
Find the area of the shaded region in the center.
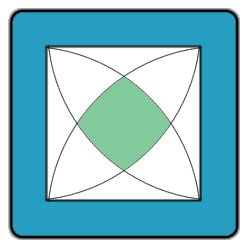
The green area can be divided into five sections - a square formed by connecting the four arc intersections and four segments (which is essentially a pie wedge with the triangle formed by the three corners hacked off).
To simplify the math, I'm going to pretend that this is a unit square on a Cartesian coordinate system with lower-left corner at the origin, and upper-right corner at (1, 1). If I can solve that problem, I'll just multiply the result I get by 49 cm² to get the result the problem is looking for.
First off, note that the triangle formed by the base of the large square and the topmost corner of the shaded area form an equilateral triangle, since all points an a circular arc are equidistant from the center. The topmost corner is thus sin(60 degrees) or √3/2 units from the bottom of the square. Its coordinates are (1/2, √3/2). The coordinates of the rightmost corner are (√3/2, 1/2). The distance between the two corners is √(2(√3/2 - 1/2)²), or (√6 - √2)/2. The area of the inscribed square I mentioned is the square of this, or 2 - √3.
Next, on to the four segments. Consider the segment between the topmost and rightmost corners. The area of that segment is the area of the pie wedge minus the area of the triangle formed by its corners. Since we know the angles are parts of equilateral triangles, the angle defined by the wedge is 30 degrees. This wedge is 1/12 of a unit circle, so its area is π/12.
All we need to do now is subtract out the area of that triangle. The area of a triangle is 1/2 x base x height. We'll consider the base of the triangle to be the line joining the top and right corners of the shaded area. We already know that its length is (√6 - √2)/2. Since its an isosceles triangle, its height is the distance from the lower-right corner to the midpoint of the base. The midpoint of the base is just the average of the two endpoints: (1/4 + √3/4, 1/4 + √3/4). Thus, the height is √(2(1/4 + √3/4)²) = (√6 + √2)/4. Thus, the area of the triangle is 1/2 x (√6 - √2)/2 x (√6 + √2)/4 = 1/4. (Hope my math's right).
The area of one segment is thus π/12 - 1/4. The area of all four segments plus the square is π/3 - 1 + 2 - √3 = 1 - √3 + π/3. Multiplying that mess by 49 cm² gives about 15.44 cm²



