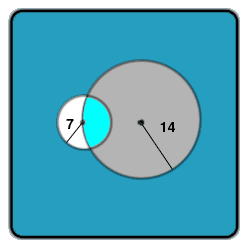
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.
(P.S -The answer might not be elegant)
(In reply to
re: by levik)
Finding length of BA:
Consider the triangle LSA (both circles' centers + one of the two intersection points). It's sides are:
LS = 14 (L's radius)
LA = 14 (L's radius)
SA = 7 (S's radius)
From this we can calculate the area if memory serves (but I don't remember the formula)
This area can also be gotten as (|LS| * |AB|/2) / 2, since AB is intersected by LS at its (AB's) midpoint. So if we have area A,
|AB| = ((A*2) / |LS|) * 2
As I don't remember the area formula, I can't actually do the math.
|
|
Posted by levik
on 2002-11-04 07:02:02 |



