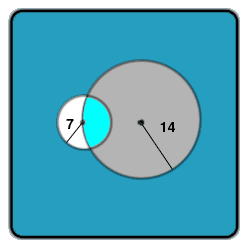
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.
(P.S -The answer might not be elegant)
(In reply to
re(2): by levik)
LSA is an isosceles triangle. Thus, the height is √(14² - (7/2)²) = 7√2² - (1/2)²) = (7/2)√15. The base is 7 cm, so the area is 1/2 x 7 x (7/2)√15 = (49/4)√15 cm².
Continuing levik's calculation,
|AB| = ((A * 2)/|LS|) * 2
=((49/2)√15/14) * 2
=(7/2)√15 cm
Angle BSA is then 2 x asin((|AB|/2)/7)
= 2 asin(√15/4)
Well, he did say the answer wouldn't be elegant. I've got a cold, and my brain hurts. Somebody want to pick it up from here?



