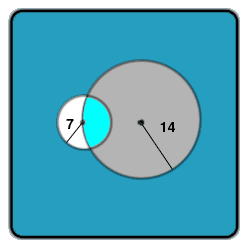
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.
(P.S -The answer might not be elegant)
Imagine the picture above placed on the coordinate system and turned around a bit so that:
big circle has its center at (0,0) of the coordinate system, and the small circle is above it with its center on the y axis.
Big circle is x^2 + y^2 = 14^2
Small circle is x^2 + (y-14)^2 = 7^2
By equating these two, we get that y = 12.25
|x| would then be |SQRT(14^2-12.25^2)| = 6.78
2x would give us the distance between the circles' intersections = 13.56
Now we calculate the sections:
1. Section in the bigger circle (center of the bigger circle, two intersections)
Angle of section is 2 x arccos (12.25/14) = 57.91
The section's area is therefore (14^2 x PI) /(360/57.91) = 99.05
The triangle's area is (13.56 x 12.25)/2, and the segment's area is 16.02
2. Section in the smaller circle (center of the smaller circle, two intersections):
Angle of section is 2 x arcsin (6.78/7) = 151.05
The section's area is (7^2 x PI) / (360/151.05) = 64.59
The triangle's area is (13.56 x (14 - 12.25))/2, and the segment's area is 52.73
Therefore, the common area is the two segments added up, which is 68.75.
(i hope the math is right)
|
|
Posted by lucky
on 2002-11-04 08:10:10 |



