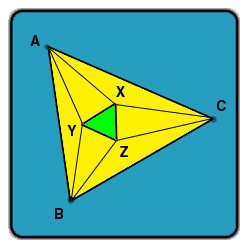
Prove or disprove, that the points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle. (In other words, that for any yellow triangle, the green triangle will be equilateral, given that the thinner lines trisect their respective angles.)

(In reply to re(2): Live by levik)

So, triangle ABC (yellow) has three angles, A, B and C.

Triangle XYZ (green) has angles X, Y and Z.

(Let's use single letter designations only for these six angles, and refer to all other angles using three letters.)

Z = 360 - (YZB + BZC + CZX)

YZB = 180 - (BYZ + YBZ) = 180 - BYZ - B/3

BZC = 180 - (ZBC + ZCB) = 180 - B/3 - C/3

CZX = 180 - (ZXC + XCZ) = 180 - ZXC - C/3

Z = 360 - (540 - BYZ - ZXC - 2(B/3) - 2(C/3))
Z = BYZ + ZXC + 2/3(B + C) - 180

Since A+B+X = 180, C + B = 180 - A and

Z = BYZ + ZXC + 2/3(180 - A) - 180
Z = BYZ + ZXC + 120 - 2(A/3) - 180
Z = BYZ + ZXC - 2(A/3) - 60

Hrm.... that looks much messier than I expected.
I am not not as sure that other angles can be easily shown to be equal.

Posted by levik on 2002-11-05 09:05:25