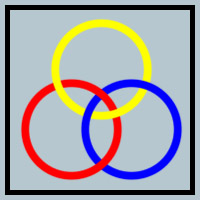
Three rings (planar circles) are "linked" together, but you'll notice that none is directly linked with another.

• The red ring is "behind" the yellow.
• The yellow ring is "behind" the blue.
• The blue ring is "behind" the red.

Still, while none is intertwined with another, it is impossible to pull them apart.
_____________________

Is this a paradox?

Can this really be built?

OK, it is clearly possible to build this IF one of the rings is flexible.  Imagine the yellow and red rings are metal, but the blue is made of string.  It's easy to see how the string could be woven in and out to make this a valid figure.  Now start to make the string progressively stiffer and more circular in shape.  The other rings will be forced to move out of the plane.  So when you consider it a 3-D object, then I think that it is possible, and the rings can not be pulled apart.

I suspect whether it is possible or not may depend on the thickness of the rings.  For very thin rings, the yellow ring can invaginate far into the red ring to perhaps make enough room for the blue ring to weave in and out.  Maybe.  What I don't know is how thin the rings have to be; for example if it turned out that the rings had to be of zero thickness, then I would say it is not possible.

Posted by Larry on 2004-05-29 12:36:18