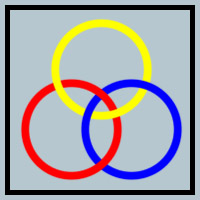
Three rings (planar circles) are "linked" together, but you'll notice that none is directly linked with another.
- The red ring is "behind" the yellow.
- The yellow ring is "behind" the blue.
- The blue ring is "behind" the red.
Still, while none is intertwined with another, it is impossible to pull them apart.
_____________________
Is this a paradox?
Can this really be built?
(In reply to
String theory by Larry)
Larry,
I think you've got it there. If the rings are flat and unbendable then this is impossible as it breaks the rule of transitivity (X<Y, Y<Z therefore X<Z). However if the rings are flexible, then certain parts of X may still be greater than Z.
So I guess my version is... yes it could be made (if the rings are alowed to bend) and if it was, then you would not be able to pull it apart.
But what I liked best about this problem was the fact that it had a picture and lots of bright colours!
 Three rings (planar circles) are "linked" together, but you'll notice that none is directly linked with another.
Three rings (planar circles) are "linked" together, but you'll notice that none is directly linked with another. 


