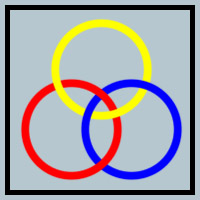
Three rings (planar circles) are "linked" together, but you'll notice that none is directly linked with another.
- The red ring is "behind" the yellow.
- The yellow ring is "behind" the blue.
- The blue ring is "behind" the red.
Still, while none is intertwined with another, it is impossible to pull them apart.
_____________________
Is this a paradox?
Can this really be built?
This shape is very much possible to make in 3 dimensions but not with rigid circular rings.
I used to make it all the time with 3 soda straws. The key with straws is to make the rings triangular or rectangular.
I can attempt to describe how to make a drawing to show how this works:
Draw a 3-D Cartesian graph. Draw three 2x4 rectangles with coordinates as follows:
(2,1,0) (2,-1,0) (-2,-1,0) (-2,1,0)
(0,2,1) (0,2,-1) (0,-2,-1) (0,-2,1)
(1,0,2) (1,0,-2) (-1,0,-2) (-1,0,2)
If you draw these rectangles first lightly, then darkening the parts in the front you can see the pattern. No two of them are actually linked at all, yet the third keeps them together.
-Jer
|
|
Posted by Jer
on 2004-05-29 16:07:19 |
 Three rings (planar circles) are "linked" together, but you'll notice that none is directly linked with another.
Three rings (planar circles) are "linked" together, but you'll notice that none is directly linked with another. 


