Prove or disprove, that the points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle. (In other words, that for any yellow triangle, the green triangle will be equilateral, given that the thinner lines trisect their respective angles.)

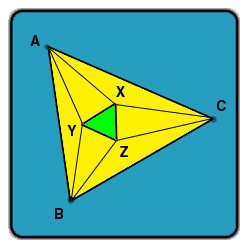
(In reply to baa by LDoc)

must be too long...okies, here's the pieces --

I've organized my angles a little differently than levik, so bear with me as I go through the givens.

GIVEN:
A+B+C= 180
YXZ+ZYX+XZY=180 (green triangle)
X + A/3 + C/3 =180 [or] X= 180 - A/3 - C/3
Y + A/3 + B/3 =180 [or] Y= 180 - A/3 - B/3
Z + B/3 + C/3 =180 [or] Z= 180 - B/3 - C/3
A/3 + AYX + AXY =180 [or] AYX+ZXY = 180 - A/3
B/3 + BZY + BYZ =180 [or] BZY+BYZ = 180 - B/3
C/3 + CZX + CXZ =180 [or] CZX+CXZ = 180 - C/3
X + CXZ + AXY + YXZ =360
Y + BYZ + AYX + ZYX =360
Z + BZY + CZX + XZY =360

Posted by LDoc on 2002-11-07 18:06:27