Prove or disprove, that the points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle. (In other words, that for any yellow triangle, the green triangle will be equilateral, given that the thinner lines trisect their respective angles.)

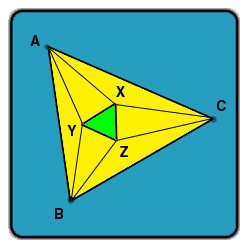
(In reply to re(2): baa by LDoc)

by adding up all the central angles around/including the green triangle you will get (feel free to check me):

YXZ + ZYX + XZY + (AXY+AYX) + (BYZ+BZY) + (CZX+CXZ) + X + Y + Z =1080
sub in the given values for the combos

YXZ + ZYX + XZY + 180 - A/3 + 180 - B/3 + 180 - C/3 + (X + Y + Z) =1080
sub in from previous solution and combine like terms:

YXZ + ZYX + XZY - A/3 - B/3 - C/3 + 300=540
(YXZ + ZYX + XZY) - A/3 - B/3 - C/3 =240
sub in given

180 - A/3 - B/3 - C/3 =240
0= 60 + (A/3 + B/3 + C/3)
sub in found result

0= 60 + 120
0=180

the situation is not possible

Posted by LDoc on 2002-11-07 18:07:28