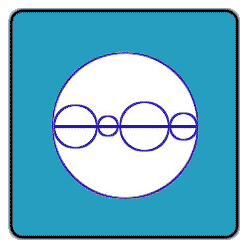
Prove that the sum of the perimeters of the smaller circles in the
Bigger circle is equal to that of the bigger circle. (The centres are on the line given which is the diameter of the bigger circle.)
This appears to be very simple.
First, label diameters in the following fashion:
d1 is the diameter of large circle, d2, d3, d4, and d5 are the diameters of the smaller circles in order from left to right (though order does not matter) and P1 is perimeter of large circle and P2, P3, P4, P5 are perimeters of the smaller circles.
We then have d1 = d2 + d3 + d4 + d5
Multiply both sides by π to get d1π = d2π + d3π + d4π + d5π
Since dπ = perimeter, d1π = P1, d2π = P2 and so on and thus, P1 = P2 + P3 + P4 + P5
Look good?





