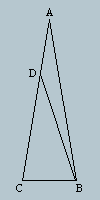
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
D is a point on side AC with AD=BC. Find angle DBC.
Solve this without trigonometry.
It's true--E must be to the upper left of the original triangle, otherwise BAE wouldn't be 100, as asserted.
Why are the angles at F 60 and 120? Notice that Triangle AEB is isoceles. (AB=AE). So, the base angles must be 40, since we already know that the vertex at A is 100. Angle AED is 20, so DEF must be 20. EDF is 100; that leaves DFE = 60. So AFB is 120.
I also noticed that AE and CB are parallel, but I don't know where that gets me.
Jim's assertion that FB = FD is what I'm having trouble with... I know it's true--I just don't see the proof.
No Subject
