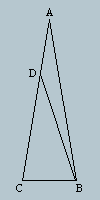
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
D is a point on side AC with AD=BC. Find angle DBC.
Solve this without trigonometry.
Here's a complete answer:
Find the point E to the upper right of the triangle such that AE = DE = AB. EDA is isoceles and congruent to ABC. Draw EB.
Angle EAD is 80 since that triangle is congruent with the original one (whose angles are 80, 80, 20). Since angle CAB = 20, angle BAE = 60. That means triangle AEB is equilateral. (two sides equal and the internal angle = 60). So angle AEB = 60, and since angle AED = 20, that makes angle BED = 40. Triangle DEB is isoceles with DE = EB (since both those sides = AE). That means angle BDE and angle DBE must each be 70 (since the vertex is 40 and the 2 base angles must be equal and the sum of the 3 angles must be 180).
Now, DE is parallel to CB because angles ADE and ACB are both 80 (corresponding angles => lines are parallel). That means angle CBD = angle BDE (parallel lines => alternate interior angles are equal), which we just showed to be 70.
So angle CBD is 70 degrees.
 Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.


