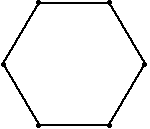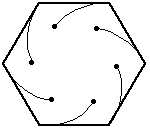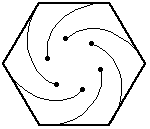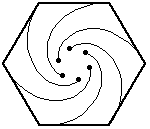
In this problem, the six bugs start at the corners of a regular hexagon (with side length=10 inches).

Again, the bugs travel directly towards their neighbor (counter-clockwise). And, again, each bug homes in on its target, regardless of its target's motion. So, their paths will be curves spiraling toward the center of the hexagon, where they will meet.

What distance will the bugs have covered by then, and how did you determine it?

I know there's a pattern here ... and a series ... and apparently these are logarithmic spirals. The series is interesting ... 0.5, 0.666667, 1, 1.44721, 2, 2.65597, 3.41421, 4.27432, 5.23607, .... it's based on the pi-cosine equation mentioned earlier and more clearly in SilverKnight's posting of 3 Bugs. The answer of 20 inches is correct here, from the series ... 2 times 10 inches=20 inches.

These are interesting though. Polygons can be extended to the circle even though pi/�� gets weird for me. What is the limit of L/1-cos(2pi/n) anyway? I have fits with limits.

The equation doesn't really work with frogs because of the discrete jumps. The frogs travel farther because the convergence is slower. It shouldn't work with people, too. Discrete steps again. Bugs and mice are better because of their tiny feet. As the steps get smaller the curve gets closer to the log spiral. If that's what it is. I'd like to find out more.