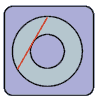
Remember this problem? The one where you had to find the area between two circles by only knowing the length of the tangent "chord" (the red line)?

That problem is solved using some (moderately) tricky geometry. But if you know that the problem is solvable, it's actually pretty easy to solve by simply using the formula for the area of the circle and a bit of logic.

Can you do it?

Chord Length =L
Inner Radius =r1
Outer Radius =r2
Area = A

Form a right triangle using 1/2 the chord, r1 from center to tangent point, and r2 from center to chord intersection of outer circle. This gives the equation,
(1/2*L)^2 + r1^2 = r2^2

The contained area follows the equation,
A=pi*r2^2 - pi*r1^2

inserting the previous solution for r2^2 gives the equation,
A=pi*[(1/2*L)^2+r1^2]-pi*r1^2

simplified gives the equation,
A=pi*(L/2)^2
where L is the lenght of the chord.

Posted by Justin on 2002-05-11 05:08:05