In a square of side 4, I pack 4 circles of unit radius.

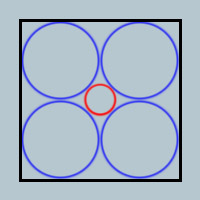
What's the largest circle I can fit into the center (such that it doesn't overlap the other circles)?

(In reply to re: Please Note by Richard)

Reiteration of  last two comments (some bold and bold italic type, and underlining, added):

Comment 10
Well, Richard, you can do this this with just one of the blue circles, too. Take the upper left one and set a 1x1 square around it. The diagonal (upper left corner to lower right corner) is clearly squareroot of 2. Subtract the unit 1 circle leaving the quarter red circle with its radius plus the same distance as that radius in the opposite corner. So, the radius = ((sqrt2)-1)/2.

Hugs. CeeAnne

Comment 9
Problem statement: In a square of side 4, I pack 4 circles of unit radius. What's the largest circle I can fit into the center (such that it doesn't overlap the other circles)?

Solution statement: Draw a square with vertices on the center of each of the big circles. The sides are 2, so the diagonal of 2sqrt(2) equals 2 plus twice the small circle's radius.So, the largest circle which can be placed has radius: sqrt(2) - 1. 
----------------------------------------------------------------------------------

Thus you see that a 1x1 square will not go around a blue circle because each blue circle has a diameter of 2.  You worked the problem with all linear distances scaled down by a factor of 2, and so your final result is scaled down by a factor of 2.

Hugably yours,

Richard 

Posted by Richard on 2004-10-20 04:37:46