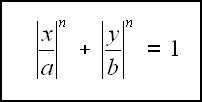There is a family of curves on the Cartesian plane described by this form:
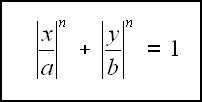
If n is equal to 2, then it describes an ellipse (if a = b, then it describes a circle).
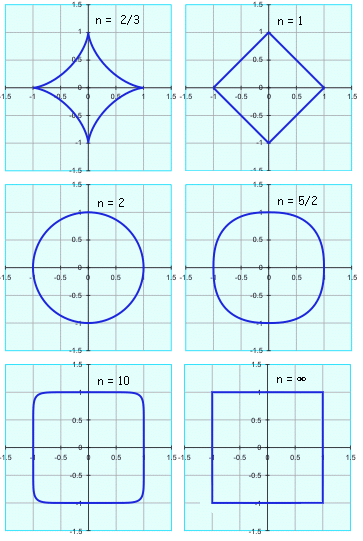
If n is greater than 2, then this is a "superellipse" (if a = b, then this is a supercircle).
As n increases, the ellipse becomes more "rectangularish", and as n approaches ∞, the limit is a rectangle (or a square if a=b).
What value must n have such that the figure has an area exactly halfway between the associated ellipse (when n=2) and rectangle (when n=∞)?
The graphs below, calculated by varying n with a = b = 1, show this property. Note that as n approaches zero, the curve degenerates into two crossed lines along the x- and y-axes.
The following program calculates the area, using Riemann sums for one quadrant and multiplying by 4, for n equal both 2 and 3.162037955231282 (the solution found--with about three more digits of precision than is warranted).
DEFDBL A-Z
CLS
incr = .0000005#
n = 2: t = 0
FOR x = incr / 2 TO 1 - incr / 2 + incr / 1000 STEP incr
t = t + incr * (1 - x ^ n) ^ (1 / n)
NEXT x
PRINT n, 4 * t
n = 3.162037955231282#: t = 0
FOR x = incr / 2 TO 1 - incr / 2 + incr / 1000 STEP incr
t = t + incr * (1 - x ^ n) ^ (1 / n)
NEXT x
PRINT n, 4 * t
It found:
2 3.141592653798805
3.162037955231282 3.570796328557276
which shows the approximation to pi (at n=2) which this particular increment (.0000005) produces, and the value found for n=3.162037955231282 using the same increment. The latter value differs from (pi+4)/2 at just about the number of places that the approximation to pi differs from pi, showing the discrepancy is due to the coarseness of the Riemann increment.
It is peculiar, as this is surely the correct answer, that Martin Gardner's "Mathematical Carnival", in the addendum to chapter 18 on Piet Hein's Superellipse, states "Norton Black, using a computer, determined that the value is a trifle greater than 3.17." Perhaps a slip of the finger from the 6 key to the 7 key?
|
|
Posted by Charlie
on 2004-10-29 02:11:20 |