Prove or disprove, that the points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle. (In other words, that for any yellow triangle, the green triangle will be equilateral, given that the thinner lines trisect their respective angles.)

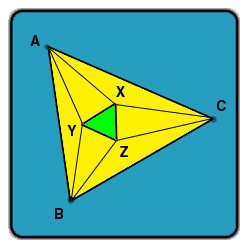
Hey Dulanjana....this problem is better known as:
" MORLEY'S THEOREM ".

here is its proof, but the problem is that I had just taken a note of the problem so the naming of the vertices of the inner triangle have been different from that given above as shown in the picture. Instead of triangle XYZ, I have taken the vertices of the inner triangle to be P,Q and R, in such a way that we get the triangles AQR, BPR and CPQ.


In triangles ARB, BPC, CQA, we know the bases - AB, BC, and AC - and the adjacent angles. The Law of Sines then yields the segments AR, BR, BP, CP, CQ, and AQ.
Next we apply the Law of Cosines to triangles AQR, BPR, and CPQ to determine (and compare) the segments QR, PR, and PQ. The fact that they come out equal proves the theorem.
For simplicity, let (angles) A = 3a, B = 3b, and C = 3c. This implies that a + b + c = 60o. Also, assuming that the radius of the circle circumscribed around ABC equals 1, we get AB = 2sin(3c), BC = 2sin(3a), AC = 2sin(3b).

Consider now BPC. By the Law of Sines,

BP/sin(c) = BC/sin(180o - b - c) = 2sin(3a)/sin(b + c) = 2sin(3a)/sin(60o - a)
Therefore, BP = 2sin(3a)sin(c)/sin(60o - a). To simplify the expression note that

sin(3a) = 3sin(a) - 4sin3(a)
= 4sin(a)[(3/2)2 - sin2(a)]
= 4sin(a)[sin2(60o) - sin2(a)]
= 4sin(a)(sin(60o) + sin(a))(sin(60o) - sin(a))
= 4sin(a) 2sin[(60o) + a)/2]cos[(60o) - a)/2] 2sin[(60o) - a)/2]cos[(60o) + a)/2]
= 4sin(a)sin(60o + a)sin(60o - a)

Reaping the fruits of this effort,

BP = 8sin(a)sin(c)sin(60o +

Posted by Ravi Raja on 2003-01-14 03:07:10