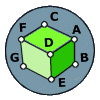
Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).

A fly, sitting in the vertex (A) of this cube must travel the surface of the cube until it arrives at the vertex (G).

If the fly cannot leave the surface of the cube, what is the shortest path for the fly to take between the two points?

I read the solution. May be its correct. We know that the shortest distance is AG ie the diagonal of the cube. But I am unable to equate distance AG to distance AD + DM + MG where M is a point between D and E, as mentioned in the solution.... Can anybody find a way to prove the solution mentioned is infact the shortest distance mathematically....

Posted by Gautam Joshi on 2003-01-16 19:29:07