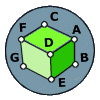
Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).
A fly, sitting in the vertex (A) of this cube must travel the surface of the cube until it arrives at the vertex (G).
If the fly cannot leave the surface of the cube, what is the shortest path for the fly to take between the two points?
(In reply to
Doubt..... by Gautam)
what i assume to be a typo in your post - the path is ato m to g, not a to d to m to g.
Despite the solution not being "mathematical", it is a full proof (to me anyways). Constructing the cube from folded paper, and then unfolding it makes it clear that this is the case. Of course, being a cube means that there are in fact 6 equivalent paths to take (not the 2 suggested in the answer) resulting in the shortest distance. The reason I would consider this to be a full proof in this case (without the mathematics), is that the situation lends itself perfectly to a 2 dimensional analysis, which then collapses to the most basic of geometries - the shortest distance between two points is a straight line - which we've been using as true for many years (hundreds?, thousands?).
re: Doubt.....
