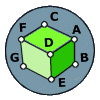
Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).
A fly, sitting in the vertex (A) of this cube must travel the surface of the cube until it arrives at the vertex (G).
If the fly cannot leave the surface of the cube, what is the shortest path for the fly to take between the two points?
(In reply to
Doubt..... by Gautam)
AG (√3) is the shortest distance, three dimensionally, but it would require the fly to somehow burrow through the cube. The problem, however, requires that the fly walks along the surface of the cube. This, in turn, allows us to unfold the cube and think two dimensionally. No matter how we unfold the cube, we wind up with two adjacent squares (the author chose ABED and EDFG) where A and G are at opposite vertices of a 2 x 1 rectangle (ABGF). The diagonal of that rectangle passes through the line segment DE at its midpoint M, and its length (√5) is the shortest two-dimensional distance from A to G
|
|
Posted by TomM
on 2003-01-17 08:20:43 |
 Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).
Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).



