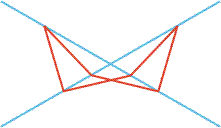
In the picture all of the red segments are of equal length and all of their endpoints lie on one of the two blue lines. Determine all possible values for the smaller angle between the blue lines.

(This problem is a special case of a problem discovered by Daniel Shapiro, professor of mathematics at Ohio State University. His problem generalizes a problem he saw years ago.)

The limits of the external conditions usually occur along with the limits of the internal conditions. So I would begin by examining the cases where

a) the point of the batwing figure toward the upper right is at (or approaches if it cannot be truly at) the upper right vertex of the rectangle (and likewise its upper left reflection),

and b) what happens when the two lower right vertices (and their lower left reflections) coincide.

 

Posted by TomM on 2005-06-08 19:41:24