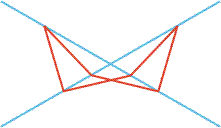
In the picture all of the red segments are of equal length and all of their endpoints lie on one of the two blue lines. Determine all possible values for the smaller angle between the blue lines.

(This problem is a special case of a problem discovered by Daniel Shapiro, professor of mathematics at Ohio State University. His problem generalizes a problem he saw years ago.)

(In reply to Label the figure by Bractals)

Ok, how about O for the intersection of the blue lines, A for the lower leftmost point where a red line meets a blue line, then moving along the closed path formed by the red lines, going upper left first, labelling red line endpoints B, C, D, E, F?  By the way, there 6 red line endpoints, not 8.

Posted by McWorter on 2005-06-09 04:08:10