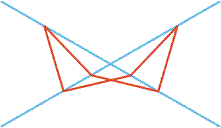
In the picture all of the red segments are of equal length and all of their endpoints lie on one of the two blue lines. Determine all possible values for the smaller angle between the blue lines.

(This problem is a special case of a problem discovered by Daniel Shapiro, professor of mathematics at Ohio State University. His problem generalizes a problem he saw years ago.)

(In reply to re: Label the figure by McWorter)

I like your labeling of the closed path.
The other two points are O (which you
specified) and the intersection of the
red lines AF and CD which I label W.

In the proof we will let the following
small letters represent the angles:

  a = <BAC = <BCA
  b = <ABC
  c = <FAE = <FEA
  d = <EDF = <EFD
  e = <DEF
  f = <CBD = <CDB
  g = <OCW
  h = <OFW
  w = <AWC = <DWF
  z = <AOB = <DOE

We want to find z.

(1) g = c+e                            (see CDE)

    g = c+w                            (see ACW)
(2) e = w                              (see 1)

(3) h = b+f                            (see FAB)

    h = f+w                            (see DFW)
(4) b = w                              (see 3)

(5) b = e                              (see 2 & 4)

    2a+b = 180                         (see ABC)
    2(f+z)+b = 180                     (see CBO)
(6) 2z = 180-b-2f

    2d+e = 180                         (see DEF)
    2(c+z)+e = 180                     (see FEO)
    2z = 180-e-2c
    2z = 180-b-2c                      (see 5)
(7) c = f                              (see 6)

    g+(180-z)+h+(180-w) = 360          (see COFW)
    (c+e)+(180-z)+(b+f)+(180-w) = 360  (see 1&3)
    z = b+(c+f)+(e-w)
(8) z = b+2f                           (see 2&7)

    3z = 180                           (add 6&8)
    z = 60

You can probably simplify the proof.

Posted by Bractals on 2005-06-09 16:17:13