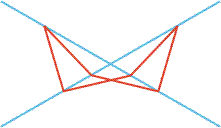
In the picture all of the red segments are of equal length and all of their endpoints lie on one of the two blue lines. Determine all possible values for the smaller angle between the blue lines.
(This problem is a special case of a problem discovered by Daniel Shapiro, professor of mathematics at Ohio State University. His problem generalizes a problem he saw years ago.)
If the verteces of the red polygon do not all have to be unique and/or
on the same side as picture of the blue lines intersection, the the
angle can range from 0º to 180º.
I assumed that these all were possible and it took me roughly four
times as long to solve. Hooray again for well-defined problems.
|
|
Posted by Charley
on 2005-06-13 08:39:58 |



