I was walking along the road one day when I spied a cord of some sort lying in my path. From my vantage point, as I was approaching the cord, I could not tell if it was knotted or not.
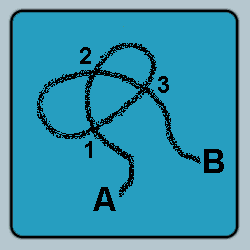
What is the probability that the cord was knotted?
(In reply to
As I figure it by Bob Smith)
I went for the brute force method too, but your post made me go back and look again. How about this:
If 1 and 2 are the same (both over or both under) then I can slide the
string at A to the left until it no longer overlaps the loop it's
either on top of or underneath. Once I do that, it's easy to see
there's no knot, because there's only one crossing. So for there to be
a knot, 1 and 2 must be *different*.
But by symmetry I can make the same argument about 2 and 3, this time
moving the string at B to the right. So for there to be a knot, 2 and 3
must be different. Well, if 1 != 2 and 2!= 3 and there are only two
options, then 1=3 and OUO and UOU are the only knots of the eight
combinations.
Actually, this isn't really rigorous because I haven't shown that OUO
or UOU is a knot, only that the other possibilities are not knots.
|
|
Posted by Paul
on 2005-08-04 02:28:04 |



