I was walking along the road one day when I spied a cord of some sort lying in my path. From my vantage point, as I was approaching the cord, I could not tell if it was knotted or not.

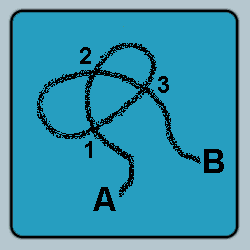
What is the probability that the cord was knotted?

(In reply to re: As I figure it by Paul)

On knots and UnknotΔ:

1) A knot is present when one cannot cannot pick up the cord by ends A and B and pull it taut so that the cord forms a straight line between the hands.
2) A knot must be formed by threading an end through a loop so that the cord entwines upon itself, running the full circumference around itself. This occurs when the 123 crossings are either OUO or UOU. Each opposite pairing represents 180 degrees of circumference that the cord has travelled about itself. 360 degrees completes a knot and since there are only three crossings, there are two possible pairs.
3) Conversely, all unknots will result in a straight-line cord when pulled taut and can be formed without having to pull an end through a loop.

* 1 follows from 2. 2 follows from 1.
3a follows from 1 and 3b follows from 2 and vice versa.

Once again, I need to take a class or two on proofs to actually prove the solution, I guess.

Edited on August 7, 2005, 3:58 am

Posted by Charley on 2005-08-05 02:51:15