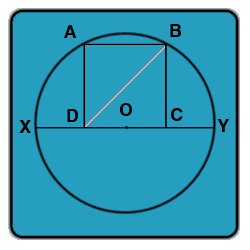
The diameter of the circle (O), (XY) is 12cm.

Two adjacent vertices of the square (ABCD) lie on the diameter of that circle, while the other two vertices lie on the circumference of the circle.

What is the length of a diagonal of this square (DB)?

Draw the radius OB. Its length is 6 cm.

Consider the right triangle BCO. Its sides are 2x, x, and 6 cm, where x is ½ the length of a side of the square, and (2x)^2 + (x^2) = (6^2) = 36.

Let S = x^2, then 5 * S = 36, or S = 7.2 (I'm not going to bother to calculate x, since I'll be squaring it again in the next step)

Now to find DB, consider that BCD is a right isosceles triange with legs = 2x.

(DB)^2 = 2 [(2x)^2] = 8 (x^2) = 8 * 7.2 = 57.6,
or DB = SQRT(57.6) = 7.6

Posted by TomM on 2002-06-02 11:35:13