Another ghost has trespassed into your haunted mansion. You are able to force him out, but only once you've caught up to him.

Both you and the other ghost take turns. During your turn, you may either stay in the same room, or move through a wall ceiling or floor to an adjacent room within the mansion (no moving diagonally). The other ghost does the same. You can sense each other's positions. The other ghost chooses the starting positions.

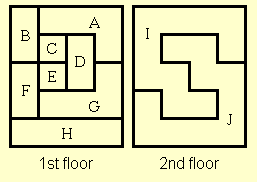
Given the above map of the mansion, can you catch the trespasser, or can he evade you indefinitely? Show a way to figure out the outcome of any given mansion.

If for any two rooms X and Y where X is not equal to Y, there exists a room Z such that X is adjacent to Z but Y is not adjacent to Z, then the Other Ghost (OG) can evade you indefinitely.

Proof: OG starts in any room and you start in any other room that is not directly adjacent to OG's. You make your move; since you did not start directly adjacent, then you cannot have won. Since you are not in the same room, by the hypothesis above there exists a room which is adjacent to OG's but not to your new room. So OG takes that. This brings us to an equivalent situation as the start, therefore OG can evade indefinitely.

Now, the above can easily be generalized to any subset S of the mansion which holds the following properties:

- It is possible to travel to every room in S without visiting a room outside of S
- The shortest path between any two rooms in S does not involve visiting a room outside of S.

I think the generalized version of this is in fact necessary, but I'm not certain.

Posted by Avin on 2006-03-08 09:48:27