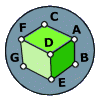
Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).
A fly, sitting in the vertex (A) of this cube must travel the surface of the cube until it arrives at the vertex (G).
If the fly cannot leave the surface of the cube, what is the shortest path for the fly to take between the two points?
The "asnwer" is already posted, but I thought I would add how to prove that the FG or DE midpoint is where the line should be bisected. One way to do this is to set up a function using the pythagorean theorem to sum the lengths of the hypotenuses travelled, and find it's minimum graphically.
D = d1 + d2
d1 = (1+dn^2)^(1/2)
d2 = (1+(1-dn)^2)^(1/2)
dn is the distance between the between the far point (F or E) and the point of bisection. D is smallest with dn = 0.5, as expected.
math, no assumptions
