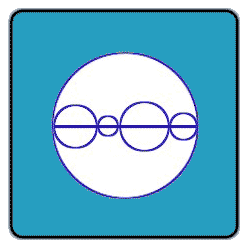
Prove that the sum of the perimeters of the smaller circles in the
Bigger circle is equal to that of the bigger circle. (The centres are on the line given which is the diameter of the bigger circle.)
Let the respective diameters of the five smaller circles be d_i, for
i=1,2,3,4,5 ; while the diameter of the bigger circle is D.
It is given that:
d_1 + d_2 + d_3 + d_4 + d_5 = D
Or, pi* (d_1 + d_2 + d_3 + d_4 + d_5) = pi*D
Or, Sum (i= 1 to 5) m_i = M_i, where m_iís is the circumference
of the ith circle for i=1,2,3,4,5 while M is the circumference of the bigger circle.
Thus, the circumference of the bigger circle is equal to the sum of the circumferences of the five smaller circles.





