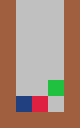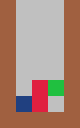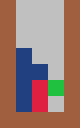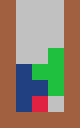perplexus.info :: Shapes : One Piece Tetris

One Piece Tetris (Posted on 2007-12-19)

A typical game of Tetris has 10 columns and 7 pieces. Consider a variation with fewer columns and only one piece, which repeats indefinitely.

For some pieces and column widths it is trivial to see that an infinite game is possible. For example the I tetromino with any column width or any other of the tetrominoes with an even column width.

For other pieces, an infinite game is possible, but not trivially so.
Consider the T tetromino in three columns, an infinite game is possible by following a pattern:
The first piece is horizontal with the stem of the T pointing down.
The second piece is vertical, with the stem of the T pointing to the right and the T is pushed to the left edge.
The third piece is vertical, with the stem of the T pointing to the left and the T is pushed to the right edge.

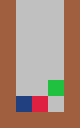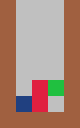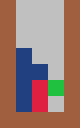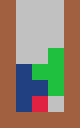
For each piece and number of columns listed below, find a strategy for each which allows for an infinite game:

1.                               2.
### in three columns             ### in four columns
#                                 #
                                  #
								  
3.                               4.
### in four columns              ##### in five columns
#                                  #
#

-----------------------------------------------------

Notes:
1 - Using the reflection of an asymmetrical piece is not allowed.
2 - Use classic gravity: when a row is filled, it is removed and all rows above move down, but no fragments of one partially filled row fall into another partially filled row.

See The Solution Submitted by Brian Smith

Rating: 4.0000 (3 votes)

Comments: ( Back to comment list | You must be logged in to post comments.)

re: case 4

Comment 5 of 5 |

(In reply to case 4 by Hugo)

My graphic program was not extensible to hexominos. The graphic block got too large for where it needed to be placed at the bottom. Extensive rewriting would have been required to have different graphic save areas for the horizontal and vertical positions.

So to play around with this, I wrote a text-based program:

DECLARE SUB clearIt (h!, p!, r!)
DECLARE SUB showIt (h!, p!, r!)
DECLARE SUB test ()
DIM SHARED grid(-5 TO 20, -2 TO 2), xVal(4, 6), yVal(4, 6), pcId

' by rot and square
xVal(1, 1) = -2
xVal(1, 2) = -1
xVal(1, 3) = 0
xVal(1, 4) = 1
xVal(1, 5) = 2
xVal(1, 6) = 0

yVal(1, 1) = 0
yVal(1, 2) = 0
yVal(1, 3) = 0
yVal(1, 4) = 0
yVal(1, 5) = 0
yVal(1, 6) = 1

FOR sq = 1 TO 6
xVal(2, sq) = yVal(1, sq)
yVal(2, sq) = xVal(1, sq)
NEXT

FOR sq = 1 TO 6
xVal(3, sq) = -xVal(1, sq)
yVal(3, sq) = -yVal(1, sq)
NEXT

FOR sq = 1 TO 6
xVal(4, sq) = -xVal(2, sq)
yVal(4, sq) = -yVal(2, sq)
NEXT

DEF fnscrnRow (y) = y + 10
DEF fnscrnCol (x) = x + 10

CLS

FOR r = 1 TO 20
LOCATE fnscrnRow(r), fnscrnCol(-3)
PRINT "| |";
NEXT
LOCATE fnscrnRow(21), fnscrnCol(-3)
PRINT "+-----+"

OPEN "tettext.txt" FOR OUTPUT AS #2
DO
rot = 1
posn = 0
ht = -3
pcId = pcId + 1

DO
showIt ht, posn, rot
DO
   a$ = INKEY$
LOOP UNTIL a$ > ""
clearIt ht, posn, rot
SELECT CASE a$
   CASE "5"
    rot = rot + 1: IF rot > 4 THEN rot = rot - 4
   CASE "4"
    posn = posn - 1
   CASE "6"
    posn = posn + 1
   CASE "2"
   CASE CHR$(27)
    END
END SELECT
LOOP UNTIL a$ = "2"
FOR row = 1 TO 20
hit = 0
FOR sq = 1 TO 6
    r = row + yVal(rot, sq)
    c = posn + xVal(rot, sq)
    IF r > 20 THEN hit = 1: EXIT FOR
    IF grid(r, c) > 0 THEN hit = 1: EXIT FOR
NEXT
IF hit THEN EXIT FOR
NEXT
row = row - 1
showIt row, posn, rot
FOR sq = 1 TO 6
   r = row + yVal(rot, sq)
   c = posn + xVal(rot, sq)
grid(r, c) = pcId
NEXT
GOSUB printIt
anyFull = 0
FOR row = 20 TO 1 STEP -1
full = 1
FOR i = -2 TO 2
    IF grid(row, i) = 0 THEN full = 0: EXIT FOR
NEXT i
IF full THEN
   anyFull = 1
   FOR j = row TO 2 STEP -1
    FOR i = -2 TO 2
      grid(j, i) = grid(j - 1, i)
    NEXT
    sRow = fnscrnRow(j)
    sRow2 = sRow - 1
    FOR i = -2 TO 2
     ch$ = CHR$(SCREEN(sRow2, fnscrnCol(i)))
     LOCATE sRow, fnscrnCol(i)
     PRINT ch$;
    NEXT
   NEXT
   row = row + 1
END IF
NEXT row
IF anyFull THEN GOSUB printIt
LOOP

END

printIt:
FOR r = 1 TO 20
   anyOn = 0
   FOR c = -2 TO 2
     IF grid(r, c) THEN anyOn = 1
   NEXT
   IF anyOn THEN
     PRINT #2, "|";
     FOR c = -2 TO 2
       IF grid(r, c) = 0 THEN
        PRINT #2, " ";
       ELSE
        PRINT #2, MID$("ABCDEFGHIJKLMNOPQRSTUVWXYZ1234567890abcdefghijklmnopqrstuvwxyz", grid(r, c), 1);
       END IF
     NEXT
     PRINT #2, "|"
   END IF
NEXT
PRINT #2, "+-----+"
PRINT #2,
RETURN

SUB clearIt (h, p, r)
ch$ = " "
FOR i = 1 TO 6
row = h + fnscrnRow(yVal(r, i))
col = p + fnscrnCol(xVal(r, i))
LOCATE row, col
PRINT ch$;
NEXT
END SUB

SUB showIt (h, p, r)
ch$ = MID$("ABCDEFGHIJKLMNOPQRSTUVWXYZ1234567890abcdefghijklmnopqrstuvwxyz", pcId, 1)
FOR i = 1 TO 6
row = h + fnscrnRow(yVal(r, i))
col = p + fnscrnCol(xVal(r, i))
LOCATE row, col
PRINT ch$;
NEXT
END SUB

SUB test
PRINT fnscrnCol(6)
END SUB

It doesn't play a real game of Tetris. The piece does not move at all until you drop it by pressing 2. The 5 key rotates it. Left and right are 4 and 6, and left and right bounds are not enforced, except by a crash if you drop outside the bounds.

A file record of the moves is created, and the following is a transcript of Hugo's method, going through its loop twice. I've annotated the beginning of the preliminary steps and the bounds of the loop.

Preliminary:

|AAAAA|
|  A  |
+-----+

|  A  |
+-----+

|BBBBB|
|  B  |
|  A  |
+-----+

|  B  |
|  A  |
+-----+

|CCCCC|
|  C  |
|  B  |
|  A  |
+-----+

|  C  |
|  B  |
|  A  |
+-----+

|DDDDD|
|  D  |
|  C  |
|  B  |
|  A  |
+-----+

|  D  |
|  C  |
|  B  |
|  A  |
+-----+

|EEEEE|
|  E  |
|  D  |
|  C  |
|  B  |
|  A  |
+-----+

|  E  |
|  D  |
|  C  |
|  B  |
|  A  |
+-----+

| FE  |
| FD  |
|FFC  |
| FB  |
| FA  |
+-----+

| FEG |
| FDG |
|FFCGG|
| FBG |
| FAG |
+-----+

| FEG |
| FDG |
| FBG |
| FAG |
+-----+

ReEntry here:

|HHHHH|
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|IIIII|
|  I  |
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|  I  |
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|JJJJJ|
|  J  |
|  I  |
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|  J  |
|  I  |
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|KKKKK|
|  K  |
|  J  |
|  I  |
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|  K  |
|  J  |
|  I  |
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|LLLLL|
|  L  |
|  K  |
|  J  |
|  I  |
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|  L  |
|  K  |
|  J  |
|  I  |
|  H  |
| FEG |
| FDG |
| FBG |
| FAG |
+-----+

|  L  |
|  K  |
|M J  |
|M I  |
|MMH  |
|MFEG |
|MFDG |
| FBG |
| FAG |
+-----+

|  L  |
|  K  |
|M J N|
|M I N|
|MMHNN|
|MFEGN|
|MFDGN|
| FBG |
| FAG |
+-----+

|  L  |
|  K  |
|M J N|
|M I N|
| FBG |
| FAG |
+-----+

|OOOOO|
|  O  |
|  L  |
|  K  |
|M J N|
|M I N|
| FBG |
| FAG |
+-----+

|  O  |
|  L  |
|  K  |
|M J N|
|M I N|
| FBG |
| FAG |
+-----+

| PO  |
| PL  |
|PPK  |
|MPJ N|
|MPI N|
| FBG |
| FAG |
+-----+

| POQ |
| PLQ |
|PPKQQ|
|MPJQN|
|MPIQN|
| FBG |
| FAG |
+-----+

| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

That completes the first cycle (pieces H through Q).

|RRRRR|
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|SSSSS|
|  S  |
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|  S  |
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|TTTTT|
|  T  |
|  S  |
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|  T  |
|  S  |
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|UUUUU|
|  U  |
|  T  |
|  S  |
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|  U  |
|  T  |
|  S  |
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|VVVVV|
|  V  |
|  U  |
|  T  |
|  S  |
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|  V  |
|  U  |
|  T  |
|  S  |
|  R  |
| POQ |
| PLQ |
| FBG |
| FAG |
+-----+

|  V  |
|  U  |
|W T  |
|W S  |
|WWR  |
|WPOQ |
|WPLQ |
| FBG |
| FAG |
+-----+

|  V  |
|  U  |
|W T X|
|W S X|
|WWRXX|
|WPOQX|
|WPLQX|
| FBG |
| FAG |
+-----+

|  V  |
|  U  |
|W T X|
|W S X|
| FBG |
| FAG |
+-----+

|YYYYY|
|  Y  |
|  V  |
|  U  |
|W T X|
|W S X|
| FBG |
| FAG |
+-----+

|  Y  |
|  V  |
|  U  |
|W T X|
|W S X|
| FBG |
| FAG |
+-----+

| ZY  |
| ZV  |
|ZZU  |
|WZT X|
|WZS X|
| FBG |
| FAG |
+-----+

| ZY1 |
| ZV1 |
|ZZU11|
|WZT1X|
|WZS1X|
| FBG |
| FAG |
+-----+

| ZY1 |
| ZV1 |
| FBG |
| FAG |
+-----+

Posted by Charlie on 2007-12-20 16:39:50

Please log in:

Login:
Password:
Remember me:

Sign up! \| Forgot password

Search:

Search body:

Forums (0)
Newest Problems
Random Problem
FAQ | About This Site
Site Statistics
New Comments (3)
Unsolved Problems
Top Rated Problems
This month's top
Most Commented On

Chatterbox:


perplexus dot info