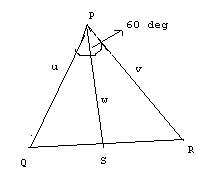
In triangle PQR, the respective length of the sides PQ and PR are denoted by u and v while the length of the median PS is denoted by w. It is known that w is the geometric mean of u and v, and Angle QPR = 60
o.
Determine |cos(Angle PQR) - cos(Angle QRP)|, where |x| denotes the
absolute value of x.
Let t = |QR|, u = |PQ|, v = |PR|, and w = |PS|.
Let <AB> denote the vector from point A to point B.
uv = w^2 = <PS> dot <PS>
<PQ> + <PR> <PQ> + <PR>
= ------------- dot -------------
2 2
u^2 + v^2 + 2uv cos(QPR)
= --------------------------
4
u^2 + v^2 + 2uv cos(60)
= -------------------------
4
or
u^2 -3uv + v^2 = 0
3 +- sqrt(5)
u = -------------- v
2
t^2 = |QR|^2 = |PQ|^2 + |PR|^2 - 2|PQ||PR|cos(QPR)
= u^2 + v^2 - 2uv cos(60) = u^2 + v^2 - uv
= 2uv
u^2 = |PQ|^2 = |PR|^2 + |QR|^2 - 2|PR||QR| cos(QRP)
= v^2 + t^2 - 2vt cos(QRP)
or
v^2 + t^2 - u^2
cos(QRP) = -----------------
2vt
v^2 = |PR|^2 = |PQ|^2 + |QR|^2 - 2|PQ||QR| cos(PRQ)
= u^2 + t^2 - 2ut cos(PQR)
or
u^2 + t^2 - v^2
cos(PQR) = -----------------
2ut
|cos(PQR) - cos(QRP)|
u^2 + t^2 - v^2 v^2 + t^2 - u^2
= | ----------------- - ----------------- |
2ut 2vt
3 |u - v| 3 sqrt(2)
= ----------- = -----------
sqrt(8uv) 4
=~ 1.06066
Edited on December 21, 2007, 8:12 pm
|
|
Posted by Bractals
on 2007-12-21 15:09:56 |
 In triangle PQR, the respective length of the sides PQ and PR are denoted by u and v while the length of the median PS is denoted by w. It is known that w is the geometric mean of u and v, and Angle QPR = 60o.
In triangle PQR, the respective length of the sides PQ and PR are denoted by u and v while the length of the median PS is denoted by w. It is known that w is the geometric mean of u and v, and Angle QPR = 60o. 


